This begins many posts on trigonometry. Trigonometry is often called circular functions in some textbooks. I have found that this topic is troublesome for many of my students. I hope you find these posts useful.
Let’s begin with the unit circle. The below picture is from Wolfram MathWorld:
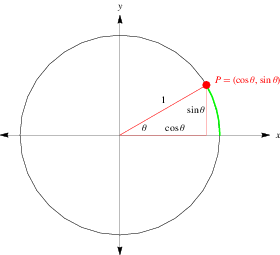
It is very important that you understand this circle as drawing it and analysing the specifics of the problem at hand will greatly add to your understanding of the problem.
The unit circle, as its name implies, is a circle of radius 1, centered at the origin of a cartesian coordinate system. A right triangle can be formed from a point on the unit circle by dropping a vertical line from the point down to the x-axis. The line from the origin to the point completes the triangle with an angle ???? from the positive x-axis. The x coordinate of the point is the length of the base of this triangle. From the basic definition of the trig function cos ????:
\[\text{cos}\ \theta \ =\frac{\text{adjacent}}{\text{hypotenuse}} =\frac{x\ \text{coordinate}}{1} =x\]Similarly,
\[\text{sin}\ \theta \ =\frac{\text{opposite}}{\text{hypotenuse}} =\frac{y\ \text{coordinate}}{1} =y\]Now I will mainly use radians as the angle measure as this is most frequently used in science and engineering. Conventionally, angles are measured from the positive x-axis. They are positive if you go counter-clockwise and negative if you go clockwise. As 2???? radians are a full circle, multiples of 2???? can be added or subtracted from an angle and you get the same angle. For example ????/4 + 2???? = 9????/4, ????/4 – 2???? = -7????/4, ????/4 + 4???? = 17????/4, ????/4 – 4???? = -15????/4. (In degrees, this is the same as adding multiples of 360°). These are all the same angle and they intersect the unit circle at the same place, so their sines are all equal as well as their cosines.
At this point, we can make some observations about the signs of the cosine, sine and tangent of an angle based on what quadrant the angle falls in. Remember that the tangent of an angle, in terms of the sine and cosine, is sin ????/cos ????:
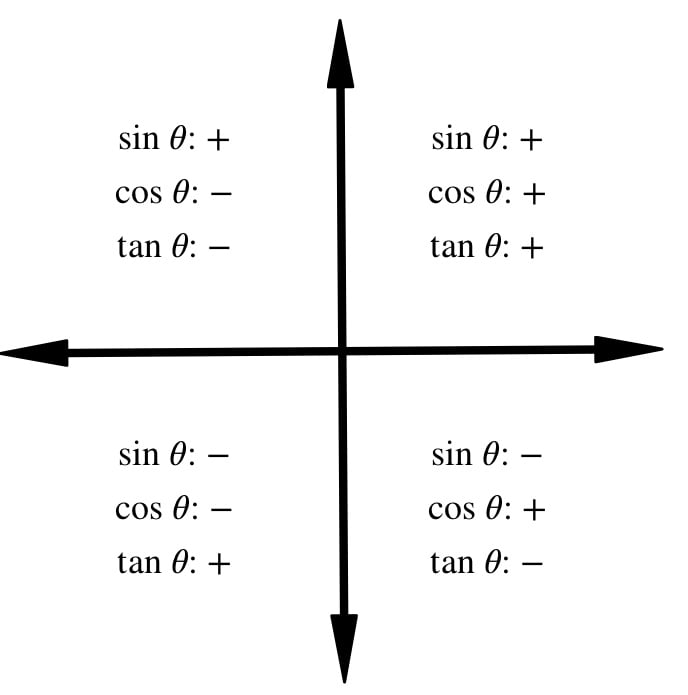
It is very important to be aware of the quadrant you are working in. When solving trigonometric equations, your calculator may give you an answer that is algebraically correct but is in the wrong quadrant based on the information from the problem at hand. I will illustrate this in future posts.
Looking the right triangle in the first figure above, remember the Pythagorean theorem that the sum of the squares of the two right angle sides equals the square of the hypotenuse. Applying this theorem to the right triangle in the figure, you get the most used trig identity, the Pythagorean Identity:
sin²(????) + cos²(????) = 1
You will probably use this enough so that you will automatically remember it.
In my next post, I will develop more trig identities which will be obvious by looking at the unit circle.
